Adjunta de una matriz

Hola nuevamente programadores un poco de teoria de:
http://es.wikipedia.org/wiki/Matriz_de_adjuntos
Dada una matriz cuadrada A, su matriz de adjuntos o matriz de cofactores cof(A) es la resultante de sustituir cada término a_ij de A por el cofactor a_ij de A. El término matriz adjunta adj(A) suele crear confusión, ya que en muchos tratados clásicos sobre álgebra lineal corresponde a la matriz de cofactores traspuesta,sin embargo, en otros textos, se corresponde a la matriz de cofactores, puesto que llaman de la misma manera adjunto al cofactor y de ahí que sea adjunta. Aparte, también se utiliza el símbolo adj( ) indistintamente a cof( ) para el cálculo en los elementos de una matriz, haciendo, si cabe, la confusión más amplia.
El interés principal de la matriz adjunta es que permite calcular la inversa de una matriz, ya que se cumple la relación:

$\mathbf{A}^{-1} = \frac{1}{\det \mathbf{A}} \; \mbox{adj}(\mathbf{A})$

donde adj(A) corresponde a la matriz de cofactores traspuesta, o sea,

$\mathrm{adj}(\mathbf{A}) = \operatorname{cof}(\mathbf{A})^T= \mathbf{C}^T \,$ .

Dada una matriz de 3 x 3:

$\mathbf{A} = \begin{pmatrix} A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} \end{pmatrix}$

Su matriz de cofactores viene dada por:

$\mbox{cof}(\mathbf{A}) = \begin{pmatrix} + \left | \begin{matrix} A_{22} & A_{23} \\ A_{32} & A_{33} \end{matrix} \right | & - \left | \begin{matrix} A_{21} & A_{23} \\ A_{31} & A_{33} \end{matrix} \right | & + \left | \begin{matrix} A_{21} & A_{22} \\ A_{31} & A_{32} \end{matrix} \right | \\ & & \\ - \left | \begin{matrix} A_{12} & A_{13} \\ A_{32} & A_{33} \end{matrix} \right | & + \left | \begin{matrix} A_{11} & A_{13} \\ A_{31} & A_{33} \end{matrix} \right | & - \left | \begin{matrix} A_{11} & A_{12} \\ A_{31} & A_{32} \end{matrix} \right| \\ & & \\ + \left | \begin{matrix} A_{12} & A_{13} \\ A_{22} & A_{23} \end{matrix} \right | & - \left | \begin{matrix} A_{11} & A_{13} \\ A_{21} & A_{23} \end{matrix} \right | & + \left | \begin{matrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{matrix} \right| \end{pmatrix} = \begin{pmatrix} A_{22}A_{33} - A_{23}A_{32} & A_{23}A_{31} - A_{21}A_{33} & A_{21}A_{32} - A_{22}A_{31}\\ A_{32}A_{13} - A_{33}A_{12} & A_{33}A_{11} - A_{31}A_{13} & A_{31}A_{12} - A_{32}A_{11}\\ A_{12}A_{23} - A_{13}A_{22} & A_{13}A_{21} - A_{11}A_{23} & A_{11}A_{22} - A_{12}A_{21} \end{pmatrix}$

y por lo tanto la transpuesta de la matriz de cofactores es la matriz Adjunta:

$\mbox{adj}(\mathbf{A}) = \begin{pmatrix} + \left | \begin{matrix} A_{22} & A_{23} \\ A_{32} & A_{33} \end{matrix} \right | & - \left | \begin{matrix} A_{21} & A_{23} \\ A_{31} & A_{33} \end{matrix} \right | & + \left | \begin{matrix} A_{21} & A_{22} \\ A_{31} & A_{32} \end{matrix} \right | \\ & & \\ - \left | \begin{matrix} A_{12} & A_{13} \\ A_{32} & A_{33} \end{matrix} \right | & + \left | \begin{matrix} A_{11} & A_{13} \\ A_{31} & A_{33} \end{matrix} \right | & - \left | \begin{matrix} A_{11} & A_{12} \\ A_{31} & A_{32} \end{matrix} \right| \\ & & \\ + \left | \begin{matrix} A_{12} & A_{13} \\ A_{22} & A_{23} \end{matrix} \right | & - \left | \begin{matrix} A_{11} & A_{13} \\ A_{21} & A_{23} \end{matrix} \right | & + \left | \begin{matrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{matrix} \right| \end{pmatrix}^T$

Para matrices de 3x3 también puede usarse la siguiente fórmula:

$[\mbox{adj}(\mathbf{A})]_{ij} = \frac{1}{2} \; \epsilon_{mni} \; \epsilon_{pqj} \; a_{mp} \; a_{nq}$

Ejemplo

Un ejemplo sería el siguiente:

$\operatorname{adj} \begin{pmatrix} 2 & 1 & 0 \\ 1 &-1 & 1 \\ 0 & 2 &-1 \end{pmatrix} = \begin{pmatrix} -1 & 1 & 1 \\ 1 &-2 &-2 \\ 2 &-4 &-3 \end{pmatrix}$

Matrices n x n

Para matrices con n grande, el costo computacional del cálculo de adjuntos es grande, por lo que si el objetivo es calcular la inversa de una matriz, se recurre a otros algoritmos de cálculos que no impliquen calcular primero la matriz de adjuntos. Para el cálculo de la matriz de adjuntos en el caso general, puede emplearse la siguiente fórmula:

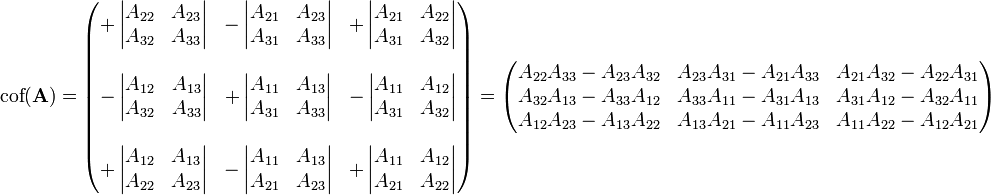
$[\mbox{adj}(\mathbf{A})]_{ij} = \frac{1}{(n-1)!} \; \epsilon_{i_1 \dots i_{n-1} i} \; \epsilon_{j_1 \dots j_{n-1} j} \; a_{i_1 j_1} \; a_{i_2 j_2} \; \dots \; a_{i_{n-1} j_{n-1}}$

Al final lo que se busca la implementacion en VB 2010 en Consola
Module Module1
    Dim A(500, 500) As Double
    Dim Adjunta(500, 500) As Double
    Dim n As Integer
    Sub Main()
        Console.BackgroundColor = ConsoleColor.White
        Console.Clear()
        Console.ForegroundColor = ConsoleColor.Black
        Console.Title = "ADJUNTA DE UNA MATRIZ"
        Console.Write(vbLf) 'Da un enter
        Console.Write("" & vbTab & " ADJUNTA DE UNA MATRIZ ")
        Console.Write(vbLf)
        Console.Write(vbLf)
        Call Ingresar()
        Call Presentar()
        Call ADJ(A)
        Call Imprimir()
    End Sub
    Sub Ingresar()
        ' Ingresa el tamaño de la matrix cuadrada
        Console.Write("" & vbTab & "Ingrese el orden de la matriz (n): ", n)
        n = Integer.Parse(Console.ReadLine())
        ' Lee los datos ingresados por teclado
        Console.WriteLine("" & vbLf & " * Ingrese los elementos de la Matriz A * " & vbLf & "")
        For i As Integer = 1 To n
            For j As Integer = 1 To n
                Console.Write("" & vbTab & "Elemento [{0},{1}] : ", i, j)
                A(i, j) = Double.Parse(Console.ReadLine()) ' Lectura de datos
            Next
        Next
    End Sub
    Sub Presentar()
        Console.WriteLine("" & vbLf & " * La Matriz A ingresada es : *" & vbLf & "")
        For i As Integer = 1 To n
            For j As Integer = 1 To n
                Console.Write("" & vbTab & "{0,2:f4}", A(i, j))
            Next
            Console.Write("" & vbLf & "")
        Next
    End Sub
    Sub ADJ(ByVal Aux(,) As Double)
        Dim A2(500, 500), MCofa(500, 500) As Double
        Dim temp, deter, mult As Double
        Dim numero, r, q, p, j, l, g As Integer
        Console.WriteLine("" & vbLf & " * La Matriz Adjunta es : " & vbLf & "")
        ' Calcula cada menor
        For p = 1 To n
            For s As Integer = 1 To n
                r = 0
                For i As Integer = 1 To n
                    q = 0
                    If p <> i Then
                        r = r + 1
                    End If
                    For j = 1 To n
                        If p <> i Then
                            If s <> j Then
                                q = q + 1
                                A2(r, q) = Aux(i, j)
                            End If
                        End If
                    Next j
                Next i
                deter = 1
                For k As Integer = 1 To n - 1
                    If A2(k, k) = 0 Then
                        For y As Integer = k To n
                            If A2(y, k) <> 0 Then
                                l = y
                                Exit For
                            End If
                        Next y
                        For m As Integer = k To n
                            temp = A2(k, m)
                            A2(k, m) = A2(l, m)
                            A2(l, m) = temp
                        Next m
                        deter = -deter
                    End If
                    For y As Integer = k + 1 To n + 1
                        If A2(y, k) <> 0 Then
                            mult = A2(y, k) / A2(k, k)
                            For m As Integer = k To n
                                A2(y, m) = A2(y, m) - A2(k, m) * mult
                            Next m
                        End If
                    Next y
                Next k
                ' Saca la determinante para cada cofactor
                For y As Integer = 1 To n - 1
                    deter = deter * A2(y, y)
                    'Calculo El Cofactor o Adjunto: Cij=(-1)^(i+j)
                    numero = (s + p)
                    For i As Integer = 1 To 100
                        numero += -2
                        If numero = 0 Then
                            g = 1
                        Else
                            If numero = 1 Then
                                g = -1
                            End If
                        End If
                    Next i
                    'Matriz de Cofactores
                    MCofa(p, s) = g * deter
                Next y
            Next s
        Next p
        'Transpone la Matriz de Cofactores
        For i As Integer = 1 To n
            For j = 1 To n
                Adjunta(i, j) = MCofa(j, i)
            Next j
        Next i
        ' ADJ = deter
    End Sub
    Sub Imprimir()
        For i As Integer = 1 To n
            For j As Integer = 1 To n
                Console.Write("" & vbTab & "{0,2:f2}", Adjunta(i, j))
            Next j
            Console.Write("" & vbLf & "")
        Next i
        Console.ReadLine()
    End Sub
End Module

Mi captura al ejecutar

Los códigos presentados por mi son, para matrices de nxn osea cuadradas. Espero tus comentarios o preguntas a mi correo, no vemos en otra publicación

Comentarios

Jorge Calderon13 de septiembre de 2013, 10:51
amigo gracias por el aporte, pero me gustaria que me explicaras como acomodar el codigo a lo visual, me refiero establecer formularios para que se aprecie visualmente elegante, como para realizar una presentacion.
ResponderEliminar
Respuestas
Jossm15 de septiembre de 2013, 20:44
Una de las formas es presentando la matriz en una grid para ser directo en una datagridview
ResponderEliminar
Respuestas
Rafael Osias27 de mayo de 2021, 9:03
Muy buena explicaciòn, gracias funciona 100%
ResponderEliminar
Respuestas