Entradas

Graficando con Microsoft Chart Control y Sql Compact 4.0

-
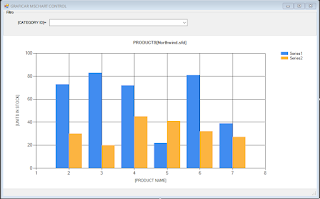
Imagen
Un saludo programadores ya en 2021 y aún conviviendo con el COVID-19 un cordial abrazo sentido a todos los que han perdido familiares, e invitar a que se protejan y lleven las normas de bioseguridad como su prioridad. Desde ya comprometido en mi hogar y en mi localidad para solventar de alguna manera esta pandemia. Entrando en tema, he preparado esta pequeña publicación para aquellos que tienen la idea o quieren aplicar graficas , ya sea estadisticas o tecnicas para cualquier ambito, es asi que el siguiente ejemplo he usado el comunmente control:Microsoft Chart Control, asi es amigos, ya que se hizo presente si mal no recuerdo para la version framework 3.0 en adelante, corríjanme si me equivoco. Ok!. Bueno el punto es que he usado la base de datos Northwind.sdf que venia por defecto en sqlcompact para demostrar un ejemplo sencillo como usar y enlazar para presentar los datos en la grafica. Primero que debemos hacer es realizar un nuevo proyecto y colocar un control Chart como lo mues
Publicar un comentario
Leer más

Error diseñador de Reportes ReportViewer en Visual Studio 2019

-
Imagen
Un saludo programadores, en esta ocasión, decidí  escribir acerca de problemas que surgen con el diseñador de Reportes en Visual Studio 2019, anteriormente en otros foros ya había leído acerca de este problema en la versión del 2017, para mi no había problema porque usaba la versión 2015, pero cuando actualice a 2017 ya lo percibí, pero asi mismo busque la ayuda de Microsoft para solventarlo.. . y fue así!. Pero al parecer VStudio con cada versión modifica el diseñador y nuevamente se presenta el problema. Al abordar la versión 2019 específicamente la 16.3.5, surgió nuevamente y creo lo parece con cada modificación. Pero bueno mas de una vez me rompió la cabeza e hice lo que solucionó con la 2017 pero con un ligero cambio, que leí en el mismo SSDT de SQL de Microsoft... https://docs.microsoft.com/en-us/sql/ssdt/download-sql-server-data-tools-ssdt?view=sql-server-2017#changes-in-ssdt-for-visual-studio-2019 Entonces el problema se ve así: El diseñador de ReportViewer se muest
3 comentarios
Leer más

Conectar base de datos Access a Devcomponents Superdatagrid Control

-
Imagen
Tras un larga temporada sin realizar un post, desde ya disculpas!...Un seguidor me ha pedido si puedo ayudarle con el tema en cuestion, para eso como ya habia hecho ejemplos relacionados, no fue dificil la peticion!... y si la realice y el codigo se expone a continuación: Primeramente el codigo que usa para coneccion, en un modulo: Module Module1 Public path As String = Form1.lblruta.Text Public conn As New OleDb.OleDbConnection("Provider=Microsoft.ACE.OLEDB.12.0;Data Source=" & path) Public cmd As New OleDb.OleDbCommand Public dr As OleDb.OleDbDataReader Public Sql As String = "" Public Sub conectarse() Try conn.Open() MsgBox("Conexion exitosa") Catch ex As Exception MsgBox(ex.ToString()) End Try End Sub Sub LlenarGrid(ByRef grid As DevComponents.DotNetBar.SuperGrid.SuperGridControl) Try ' conectarse() Dim dt As New DataT
Publicar un comentario
Leer más

Subir archivos a MEGA desde Visual Basic Net --Actualizado mayo 2017--

-
Imagen
Un saludo a todos mis seguidores de la programación vbnet, hace un tiempo acá esa un poco perdido en esto de los post, pero como Uds saben todos tenemos ocupaciones que a veces nos conllevan al descuido de otras. Pero qui me encuentro con todo el ánimo de seguir compartiendo, eso si códigos importantes que ayuden de forma significativa a los cibernautas. Como dice el tema de este post,"Subir archivos a MEGA desde Visual Basic Net", tratar de subir archivos a mega que bien nos caería para nuestra aplicación sobre todo si quisiéramos respaldar alguna base de datos tipo access, compact, sqlite medianamente conectada y/o archivos como imágenes, videos, etc. Pues bien siguiendo en el desarrollo de este tema y siendo para mi bastante importante me encamine en buscar información relevante al tema y para los que no gustan de otro lenguaje, para vb no había o tal vez no supe buscar bien, en fin... Opte por modificar un ejemplo que ya nos venia. que Uds también pueden chequear y tra
3 comentarios
Leer más

Metodo Iterativo Gauss-Seidel en Visual Basic

-
Imagen
Un cordial saludo programadores y matemáticos a fin. En esta entrega hacemos mención a la resolución de ecuaciones simultaneas por métodos iterativos y es así que el método de Gauss-Seidel se acopla muy bien como una mejora al método de Jacobi, sin embargo la condicion fundamental  que su diagonal principal debe ser mayor a las demas. Por todo lo expresado aqui presento un poco de teoria tomado de   http://www.jldelafuenteoconnor.es/Clase_itera_2016.pdf  en el cual se expresan algunos métodos más pero para este tema analizaremos solamente el mencionado. La implementación en visual Basic 2015 Module Module1 Dim A(500, 500) As Single Dim B(500, 500) As Single Dim X(500, 500) As Single Dim n, iter As Integer Dim cError, Tol, sum As Double Sub Main() Console.BackgroundColor = ConsoleColor.White Console.Clear() Console.ForegroundColor = ConsoleColor.Black Console.Title = "METODO ITERATIVO GAUSS-SEIDEL"
1 comentario
Leer más

Metodo Muller en Visual Basic

-
Imagen
Saludos programadores, detro de los métodos numéricos para hallar raíces polinomiales tenemos este método "Metodo de Muller".les dejo un estracto de teoria de mi libro y la implementacion del mismo en Visual Basic Aquí les presento la implementación Public Class Form1 Dim imax As Integer, iter As Integer Dim h As Double, xr As Double, eps As Double Sub Muller(ByVal xr, ByVal h, ByVal eps, ByVal maxit, ByVal iter) Dim x0 As Double, x1 As Double, x2 As Double Dim h0 As Double, h1 As Double, d0 As Double, d1 As Double Dim a As Double, b As Double, c As Double Dim den As Double, rad As Double, dxr As Double x2 = xr x1 = xr + h * xr x0 = xr - h * xr Do iter = iter + 1 h0 = x1 - x0 h1 = x2 - x1 d0 = (f(x1) - f(x0)) / h0 d1 = (f(x2) - f(x1)) / h1 a = (d1 - d0) / (h1 + h0) b = a * h1 + d1 c = f(x2) rad = Math.Sqrt(b * b - 4 * a * c) If Math.Abs(b + rad) > Math.Abs(b - rad) Then den = b + rad Else den = b - rad End If dxr = -2 * c / den xr = x2 + dxr If Math.Abs(dxr) &
5 comentarios
Leer más

DevComponents-Supergrid Maestro-detalle con base de datos SQL Compact 4.0

-
Imagen
Que tal amigos programadores vb, en esta ocasión, les describo como mostrar el tipo Maestro-detalle usando el control supergrid que viene con el paquete de Dotnetbar Devcomponents. Aunque en los ejemplos que trae consigo este paquete, no siempre es fácil tratar de acoplarlo a nuestras necesidades con la mayor sencillez posible, siendo así les muestro como presentarlo de forma muy simple, tomando como base de datos una que yo tengo para mi uso y que la voy a incluir en este ejemplo. Pues bien, le presento el código completo: Dentro del modulo de llamada a la base de datos "CREDIT.sdf" Module Module1 Public path As String = System.AppDomain.CurrentDomain.BaseDirectory + "CREDIT.sdf" Public conn As New SqlServerCe.SqlCeConnection("Data Source=" & path + ";Password=database1;Max Database Size=4091") Public sql As String Public cmd As New SqlServerCe.SqlCeCommand(sql, conn) Public Sub conectarse() Try c
3 comentarios
Leer más