Método de Newton-Raphson con Visual Basic
Que tal programadores hoy les presento un tema de ingeniería propio de mi libro, que aun tengo en redacción.
Texto tomado de wikipedia
El método de Newton-Raphson es un método abierto, en el sentido de que no está garantizada su convergencia global. La única manera de alcanzar la convergencia es seleccionar un valor inicial lo suficientemente cercano a la raíz buscada. Así, se ha de comenzar la iteración con un valor razonablemente cercano al cero (denominado punto de arranque o valor supuesto). La relativa cercanía del punto inicial a la raíz depende mucho de la naturaleza de la propia función; si ésta presenta múltiples puntos de inflexión o pendientes grandes en el entorno de la raíz, entonces las probabilidades de que el algoritmo diverja aumentan, lo cual exige seleccionar un valor puesto cercano a la raíz. Una vez que se ha hecho esto, el método linealiza la función por la recta tangente en ese valor supuesto. La abscisa en el origen de dicha recta será, según el método, una mejor aproximación de la raíz que el valor anterior. Se realizarán sucesivas iteraciones hasta que el método haya convergido lo suficiente.
Sea f: [a, b] -> R función derivable definida en el intervalo real [a, b]. Empezamos con un valor inicial x0 y definimos para cada número natural n
Donde f ' denota la derivada de f.
Nótese que el método descrito es de aplicación exclusiva para funciones de una sola variable con forma analítica o implícita conocible. Existen variantes del método aplicables a sistemas discretos que permiten estimar las raíces de la tendencia, así como algoritmos que extienden el método de Newton a sistemas multivariables, sistemas de ecuaciones, etc.
Estimación del Error
Se puede demostrar que el método de Newton-Raphson tiene convergencia cuadrática: si  es raíz, entonces:
es raíz, entonces:
 es raíz, entonces:
es raíz, entonces:
para una cierta constante  . Esto significa que si en algún momento el error es menor o igual a 0,1, a cada nueva iteración doblamos (aproximadamente) el número de decimales exactos. En la práctica puede servir para hacer una estimación aproximada del error:
. Esto significa que si en algún momento el error es menor o igual a 0,1, a cada nueva iteración doblamos (aproximadamente) el número de decimales exactos. En la práctica puede servir para hacer una estimación aproximada del error:
 . Esto significa que si en algún momento el error es menor o igual a 0,1, a cada nueva iteración doblamos (aproximadamente) el número de decimales exactos. En la práctica puede servir para hacer una estimación aproximada del error:
. Esto significa que si en algún momento el error es menor o igual a 0,1, a cada nueva iteración doblamos (aproximadamente) el número de decimales exactos. En la práctica puede servir para hacer una estimación aproximada del error:
Error relativo entre dos aproximaciones sucesivas:
Con lo cual se toma el error relativo como si la última aproximación fuera el valor exacto. Se detiene el proceso iterativo cuando este error relativo es aproximadamente menor que una cantidad fijada previamente.
Ejemplo
Consideremos el problema de encontrar un número positivo x tal que cos(x) = x3. Podríamos tratar de encontrar el cero de f(x) = cos(x) - x3.
Sabemos que f '(x) = -sin(x) - 3x2. Ya que cos(x) ≤ 1 para todo x y x3 > 1 para x>1, deducimos que nuestro cero está entre 0 y 1. Comenzaremos probando con el valor inicial x0 = 0,5
Los dígitos correctos están subrayados. En particular, x6 es correcto para el número de decimales pedidos. Podemos ver que el número de dígitos correctos después de la coma se incrementa desde 2 (para x3) a 5 y 10, ilustrando la convergencia cuadrática.
Implementación en Visual Basic
Public Class Form1
Dim iter, imax As Integer 'Declaración de variables
Dim xrold, xr, xi, er, dfxi, fxi, x0, tol As Double
Function NewtonR(ByVal xi) As Double
imax = 100
iter = 1
tol = 0.00001
Do While iter <= imax
xrold = xr
fxi = Math.Cos(xi) - (xi ^ 3)
dfxi = -Math.Sin(xi) - (3 * (xi ^ 2))
If dfxi = 0 Then
MsgBox("La derivada f'(x)=0, no se puede realizar el calculo", MsgBoxStyle.Critical)
Exit Do
End If
xr = xi - (fxi / dfxi)
If xr <> 0 Then
er = Math.Abs((xr - xrold) / xr) '* 100
End If
xi = xr 'Actualiza xi
Dim lvi As ListViewItem = Me.ListView1.Items.Add(iter)
lvi.SubItems.Add(xr) 'Impresión de resultados
lvi.SubItems.Add(er)
lvi.SubItems.Add(fxi)
lvi.SubItems.Add(dfxi)
iter = iter + 1
If er <= tol Then
Exit Do
End If
If Not er <= tol And iter > imax Then
MsgBox("El metodo fracaso despues de " & iter & " iteracion(es)", MsgBoxStyle.Critical)
End If
Loop
NewtonR = xr
End Function
Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click
x0 = 0.5
Call NewtonR(x0)
End Sub
End Class
Y es todo. Nos vemos en otra entrega!
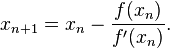
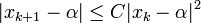
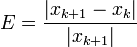




como puedo hacer para ingresar la función y calcule solo la derivada hay algún codigo para calcular la derivada?
ResponderEliminar